Techyrack Hub

Is ReFT All We Needed?


Representation Fintuning — Beyond the PEFT Techniques for fine-tuning LLMs

Hasn’t everyone started using ReFT yet?

Stanford published the paper ReFT: Representation finetuning for language models in May 2024, which immediately showed its great potential. In July 2024, Oxen.ai presented an experiment finetuning Llama3 (8B) on a single Nvidia A10 GPU within 14 mins, further demonstrating this technique's power.

Unlike SOTA PEFT methods, which focus on modifying the model weights or input, the ReFT technique is based on a previously proposed distributed interchange intervention (DII) method. The DII method first projects the embedding from the deep learning model to a lower dimension subspace and then interferes through the subspace for fine-tuning purposes.

In the following, we’ll first walk the readers through SOTA fine-tuning PEFT algorithms such as LoRA, prompt tuning, and prefix tuning; then we’ll discuss the original DII method to provide a better context for understanding; lastly, we’ll discuss the ReFT technique and present the results from the paper.

Image source: https://pxhere.com/en/photo/1377005

PEFT — Parameter Efficient Finetuning Techniques

Hugging Face has a blog detailing different PEFT techniques for fine-tuning LLMs. Here, we quickly recap these techniques.

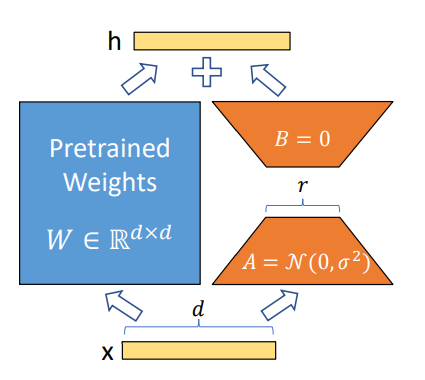
Proposed in 2021, LoRA has become one of the most successful techniques for fine-tuning LLMs and diffusion models (e.g., Time-varying LoRA) due to its simplicity and generalization ability. The idea is simple: instead of fine-tuning the original weight parameters for each layer, the LoRA technique adds two low-rank matrices and only finetunes the low-rank matrices. The trainable parameters could be reduced to less than 0.3% during fine-tuning of the whole network, which significantly speeds up the learning process and minimizes the GPU memory.

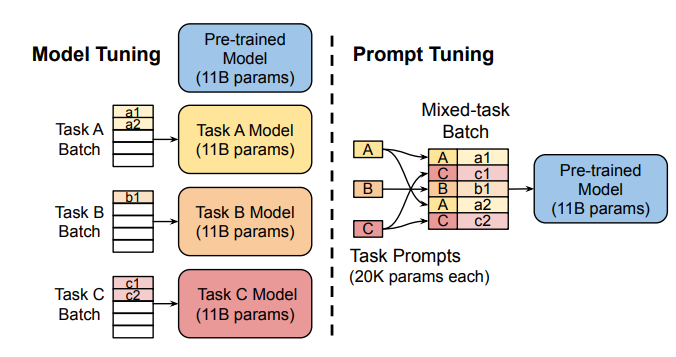
LoRA model update. Image source: https://arxiv.org/pdf/2106.09685

Instead of changing the pre-trained model’s inner layers, the Prompt Tuning technique proposed to use “soft prompts,” a learnable task-specific prompt embedding as a prefix. Given mixed-task batch prompts, the model could efficiently perform multi-task prediction without extra task-specific model copy (as against the Model Tuning in the following left sub-figure).

Prompt tuning vs classical model finetuning. Image source: https://arxiv.org/pdf/2104.08691

To provide universality for prompt tuning models at scales (e.g., over 10B parameters), Prefix Tuning (P-Tuning v2) proposed to prefix trainable prompt embeddings at different layers, which allows learning task-specific information at various scales.

Multi-scale prompts for P-tuning v2. Image source: https://arxiv.org/pdf/2110.07602

Among all these PEFT techniques, LoRA is the most widely used in fine-tuning LLMs for its robustness and efficiency. A detailed empirical analysis can be found in this paper.

Distributed Interchange Intervention (DII)

Causal abstraction is a robust artificial intelligence framework that uses the intervention between a causal model (a high-level model) and a neural network model (or a low-level model) to induce alignment estimation. If there exists an alignment between the two models, we know the underlying mechanisms between the causal model and the NN are the same. The approach of discovering the underlying alignment by intervention is called interchange intervention (II), which is intuitively explained in this lecture video.

However, classical causal abstraction uses brute force to search through all possible alignments of model states, which is less optimal. A Distributed Interchange Intervention (DII) system first projects high-level and low-level models to sub-spaces through a series of orthogonal projections and then produces an intervened model using certain rotation operations. A fascinating intervention experiment on vision models can be found here.

More specifically, the DII could be written as the following:

Equation source: https://arxiv.org/pdf/2404.03592

Where R is a low-rank matrix with orthogonal rows, indicating orthogonal projections; b and s are two different representations encoded by the model from two different inputs; the intervention will happen on the low-rank space, e.g., the space that contains Rs and Rb; the projection matrix R will be further learnt by distributed alignment search (DAS), which optimizes towards “the subspace that would maximize the probability of expected counterfactual output after intervention.”

ReFT — Representation Fintuning

Thus, the ReFT technique could be seen as the intervention of the model's hidden representation in a lower dimension space, as illustrated below, where \phi is the intervention and directly applied to the hidden representation at layer L and position P:

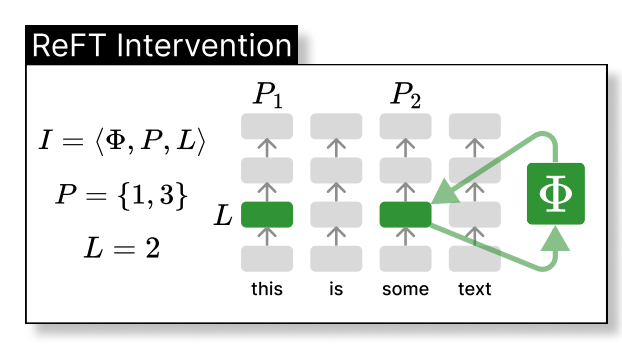
ReFT intervention at a high level. Image source: https://arxiv.org/pdf/2404.03592

Specifically, the paper further proposes a Low-rank Linear Subspace Reft (LoReFT), which further introduces a learnt projected source:

Equation source: https://arxiv.org/pdf/2404.03592

Where h is the hidden representation, (Rs = Wh + b) is the learnt protected source, which edits the representation h in the projected low-dimension space spanned by R. Now, we can illustrate the LoReFT in the original deep neural network layer below.

Image source: https://arxiv.org/pdf/2404.03592

When fine-tuning on an LLM, the parameters of the LM are kept frozen while only the parameters of the projection \phi={R, W, b} are trained.

Experiments

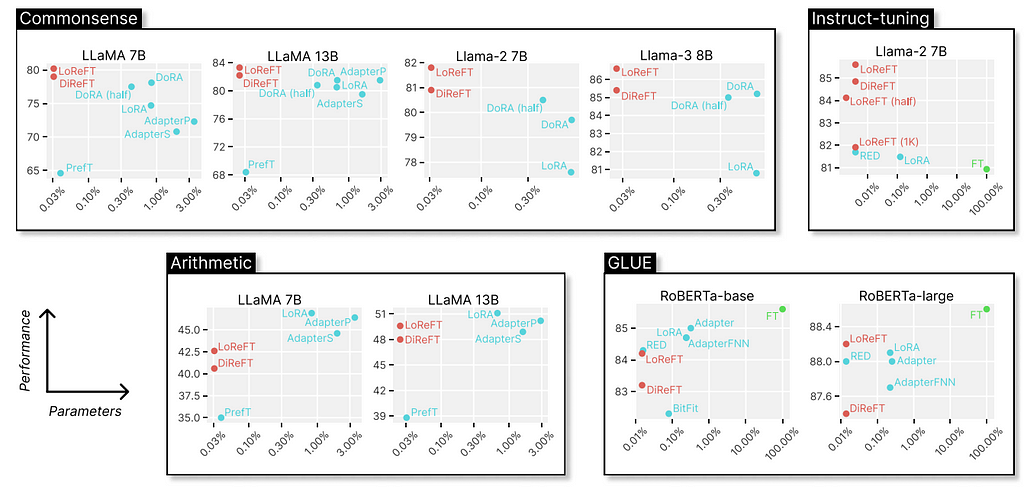
The original paper shows experiments comparing the LoReFT (and other techniques from the ReFT family) to full fine-tuning (FT), LoRA, Prefix-tuning, etc., on four types of benchmarks: common-sense reasoning, arithmetic reasoning, instruction following, and natural language understanding. We can see that, compared to LoRA, the ReFT techniques further reduce the parameters by at least 90% while achieving higher performance by a large margin.

Image souce: https://arxiv.org/pdf/2404.03592

Discussions

Why is ReFT so fascinating? Firstly, the technique provides convincing results with Llama-family models on various benchmarks outperforming the SOTA fine-tuning methods. Secondly, the technique is deeply rooted in the causal abstraction algorithm, which offers further ground for model interpretation, especially from the hidden representation’s perspective. As mentioned in the original paper, ReFT shows that “a linear subspace distributed across a set of neurons can achieve generalized control over a vast number of tasks,” which might further open doors for helping us better understand large language models.

References

Is ReFT All We Needed? was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.